|
home | what's new | other sites | contact | about |
||
|
Word Gems exploring self-realization, sacred personhood, and full humanity
Editor’s collection of notes: Pre-Algebra Distributive Property: Multiplication over Addition, Subtraction
return to "mathematics:notes" main-page
What is the Distributive Property in Arithmetic and Algebra? Named the Distributive Property (sometimes referred to as the distributive law) because in essence, you are distributing something as you separate or break it into parts. The distributive property makes numbers easier to work with. In algebra when we use the distributive property, we're expanding (distributing). The Distributive Property in Arithmetic: The Distributive Property lets you multiply a sum by multiplying each addend separately and then add the products. The Distributive Property helps with mental math and should be taught to children as a method to multiply much quicker in their heads. Children need lots of experience using the Distributive Property. Children make greater 'connections' with the ability to use the distributive property for mental math. For instance: Let's say I have to quickly multiply: 4 x 53 In my mind, I can compute the answer of 4x50 quickly (200) then I add (4x3) 12 to give me 212. That's why using the Distributive property can come in handy! Let's try another: 12x19 - Well 12 x 20 is easy, it's 240 But, I added one more 12 than I needed, so I'll take it away from 240 to give me 228. 4 x 27
Distributive property of multiplication over subtraction is a very useful property that lets us simplify expressions in which we are multiplying a number by the difference of two other numbers. The property states that the product of a number and the difference of two other numbers is equal to the difference of the products. More clearly, 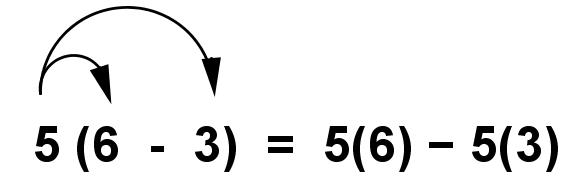
it's the distributive law of multiplication over addition and subtraction The Distributive Law says that multiplying a number by a group of numbers added together is the same as doing each multiplication separately. Example: 3 × (2 + 4) = 3×2 + 3×4. So the “3” can be “distributed” across the “2+4” into 3 times 2 and 3 times 4. changes the grouping of items, but total remains the same: What a strange world it would be if you could have more or less than 25 cents based on how you grouped them! allows rewriting of an expression as an identical form easier to work with in some way To “distribute” means to divide something or give a share or part of something. According to the distributive property, multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together. you are distributing something as you separate or break it into parts; 4 x 53 vs. 4(50 + 3); makes numbers easier to work with. lets you multiply a sum by multiplying each addend separately and then add the products; helps with mental math 4(50 + 3) = you are distributing the 4 to each of the addends; instead of 4 x 53, allows the factor 4 to multiply each place value separately works in two directions; (1) to find the product 3(5+2), mult. is distrib. over addition. (2) or, a common factor can be removed from the terms: 3*5 + 3*2 = 3(5+2) a way of eliminating a set of grouping symbols the Commutative, Associative, and Distributive Properties can be used to rearrange expressions if this is to one's advantage in problem solving
|
||
|
|